[Papers] Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism

[Link to Paper] Megatron-LM

PAPER SUMMARY

PROBLEM	Current large NLP models require additional memory management techniques
SOLUTION	Model parallel approach using intra-layer model parallelism

 

 

 

---

BACKGROUND

Data Parallelism in Deep Learning

Training minibatch is split across multiple workers

• Problem: Model must fit entirely on one worker

Model Parallelism in Deep Learning

Memory usage and computation of a model is distributed across multiple workers

1. Pipeline model parallelism

• groups of operations are performed on one device before outputs are passed to the next device, where a differenc group of operations are performed
• Using synchronized logic (e.g. GPipe) to handle inconsistencies $\Rightarrow$ need additional logic

2. Distributed tensor computation

• Partition a tensor operation across multiple GPUs to accelerate computation

 

 

---

Model Parallel Transformers

Transformer architecture

 

MLP block

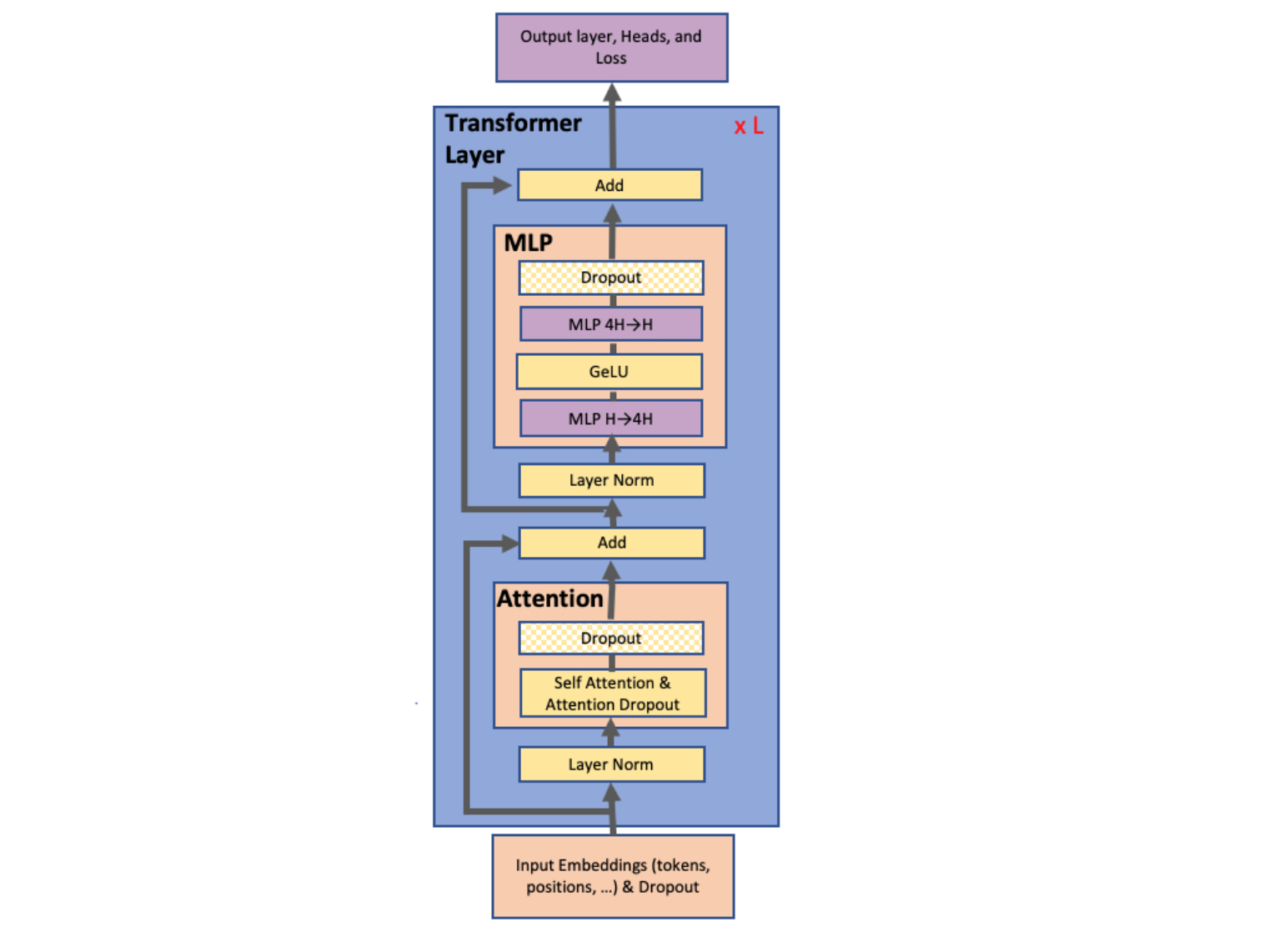
MLP block

$GEMM$ followed by $GeLU$ nonlinearity : $Y=GeLU(XA)$

• Parallelizing $GEMM$ :
  • <option1 - split along rows> make $X=[X_1, X_2]$ and $A=[A_1,A_2]^T$
    • $GeLU$ is a nonlinear function, so $Y=GeLU(X_1A_1+X_2A_2)\neq GeLU(X_1A_1)+GeLU(X_2A_2)$
    • need synchronization point before $GeLU$ function
  • <option2 - split along columns> make $A=[A_1,A_2]$
    • allow independent appliance; $[Y_1,Y_2]=[GeLU(XA_1),GeLU(XA_2)]$
    • advantageous because it removes the synchronization point
• apply <option2> on first MLP layer, and <option1> on second MLP layer
  • possible to take output of $GeLU$ layer without communication
• require only single all-reduce operation in forward & backward passes respectively

 

Self-Attention block

Self-Attention block

 

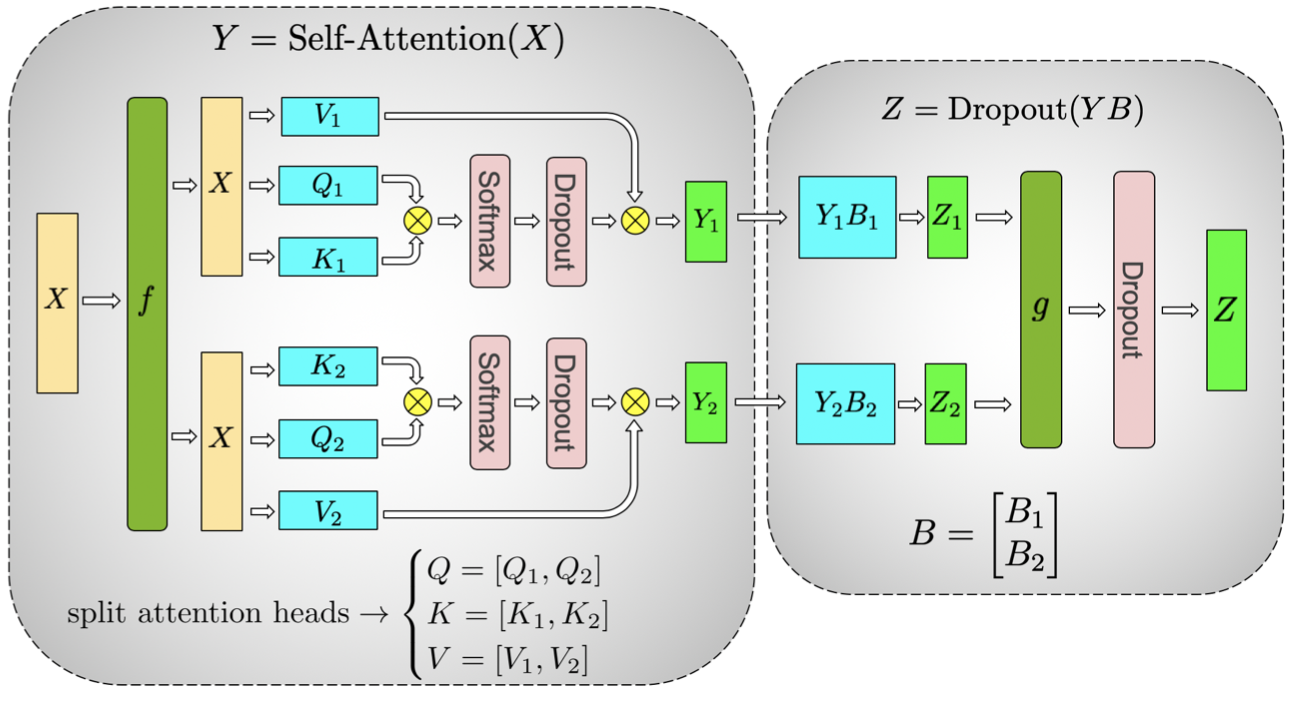
• apply the $GEMM$ optimization to $Q, K, V \Rightarrow $ matrix multiply corresponding to each attention head is done on one GPU
  • not require immediate communication

 

Summary: In both blocks, the above algorithm eliminates a synchronization point in between

 

 

Input Embedding Weight Matrix

• parallelize input embedding along vocabulary dimension $E=[E_1,E_2]$ by perform parallel $GEMM[Y_1,Y_2]=[XE_1,XE_2]$ to obtain logits
  • but, $allGather[Y_1,Y_2]$ and sending result to cross-entropy communicates $b$ x $s$ x $v$ elemnts
  • thus, fuse $GEMM$ with cross entropy $\Rightarrow$ reduce dimension to $b$ x $s$

 

---